Trilobites revived: fragile Rydberg molecules, Coulomb Green’s function, Lambert’s theorem

The trilobite Rydberg molecule can be modeled by the Coulomb Green’s function, which represents the quantized version of Lambert’s orbit determination problem.

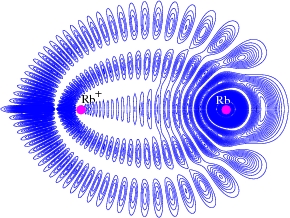
The recent experimental realization observation of giant Rydberg molecules by Bendkowsky, Butscher, Nipper, Shaffer, Löw, Pfau [theoretically studied by Greene and coworkers, see for example Phys. Rev. Lett. 85, 2458 (2000)] shows Coulombic forces at work at large atomic distances to form a fragile molecule. The simplest approach to Rydberg molecules employs the Fermi contact potential (also called zero range potential), where the Coulomb Green’s function plays a central role. The quantum mechanical expression for the Coulomb Green’s function was derived in position space by Hostler and in momentum space by Schwinger. The quantum mechanical expression does not provide immediate insights into the peculiar nodal structure shown on the left side and thus it is time again to look for a semiclassical interpretation, which requires to translate an astronomical theorem into the Schrödinger world, one of my favorite topics.

Johann Heinrich Lambert was a true “Universalgelehrter”, exchanging letters with Kant about philosophy, devising a new color pyramid, proving that π is an irrational number, and doing physics. His career did not proceed without difficulties since he had to educate himself after working hours in his father’s tailor shop. After a long journey Lambert ended up in Berlin at the academy (and Euler choose to “escape” to St. Petersburg).

Lambert followed Kepler’s footsteps and tackled one of the most challenging problems of the time: the determination of celestial orbits from observations. In 1761 Lambert did solve the problem of orbit determination from two positions measurements. Lambert’s Theorem is a cornerstone of astronavigation (see for example the determination of Sputnik’s orbit using radar range measurements and Lambert’s theorem). Orbit determination from angular information alone (without known distances) is another problem and requires more observations.

Lambert poses the following question [Insigniores orbitae cometarum proprietates (Augsburg, 1761), p. 120, Lemma XXV, Problema XL]: Data longitudine axis maioris & situ foci F nec non situ punctorum N, M, construere ellipsin [Given the length of the semi-major axis, the location of one focal point, the points N,M, construct the two possible elliptical orbits connecting both points.]

Lambert’s construction to find all possible trajectories from N to M and to map them to a ficticious 1D motion from n to m.

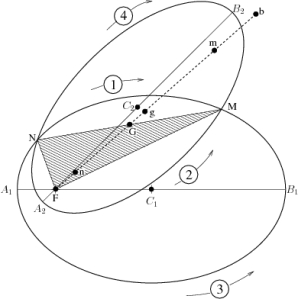
Lambert finds the two elliptic orbits [Fig. XXI] with an ingenious construction: he maps the rather complicated two-dimensional problem to the fictitious motion along a degenerate linear ellipse. Some physicists may know how to relate the three-dimensional Kepler problem to a four-dimensional oscillator via the Kustaanheimo–Stiefel transformation [see for example The harmonic oscillator in modern physics by Moshinsky and Smirnov]. But Lambert’s quite different procedure has its advantages for constructing the semiclassical Coulomb Green’s function, as we will see in a moment.

Shown are two ellipses with the same lengths of the semimajor axes 1/2 A₁B₁=1/2 A₂ B₂ and a common focus located at F. The centers of the two ellipses are denoted by C₁ and C₂. Lambert’s lemma allows to relate the motion from N to M on both ellipses to a common collinear motion on the degenerate linear ellipse Fb, where the points n and m are chosen such that the time of flight (TOF) along nm equals the TOF
along the elliptical arc NM on the first ellipse. On the second ellipse the TOF along the arc NB₂M equals the TOF along nbm. The points n and m are found by marking the point G halfway between N and M. Then the major axis Fb=A₁ B₁=A₂ B₂ of the linear ellipse is drawn starting at F and running through G. On this line the point g is placed at the distance Fg=1/2(FN+FM). Finally n and m are given by the intersection points of a circle around g with radius GN=GM. This construction shows that the sum of the lengths of the shaded triangle α_±=FN + FM ± NM is equal to α_±=fn+ fm ± nm. The travel time depends only on the distances entering α_±, and all calculations of the travel times etc. are given by one-dimensional integrations along the ficticious linear ellipse.

Lambert did find all the four possible trajectories from N to M which have the same energy (=semimajor axis a), regardless of their eccentricity (=angular momentum). The elimination of the angular momentum from Kepler’s equation is a tremendous achievement and the expression for the action is converted from Kepler’s form

• [Kepler] W(r,r‘;E)=√μ a K_c [ξ + ε sin(ξ) – ξ’ – ε sin(ξ’)], with eccentricity ε, eccentric anomaly ξ to
• [Lambert] W(r,r‘;E)=√μ a K_c[γ + sin(γ) – δ – sin(δ)], with
  sin²(γ/2)=(r+r’+ |r‘-r|)/(4a) and sin²(δ/2)=(r+r’- |r‘-r|)/(4a).

The derivation is also discussed in detail in our paper [Kanellopoulos, Kleber, Kramer: Use of Lambert’s Theorem for the n-Dimensional Coulomb Problem Phys. Rev. A, 80, 012101 (2009), free arxiv version here]. The Coulomb problem of the hydrogen atom is equivalent to the gravitational Kepler problem, since both are subject to a 1/r potential. Some readers might have seen the equation for the action in Gutzwiller’s nice book Chaos in classical and quantum mechanics, eq. (1.14). It is worthwhile to point out that the series solution given by Lambert (and Gutzwiller) for the time of flight can be summed up easily and is denoted today by an inverse sine function (for hyperbolic motion a hyperbolic sine, a function later introduced by Riccati and Lambert). Again, the key-point is the introduction of the linear ficticious ellipse by Lambert which avoids integrating along elliptical arcs.

The surprising conclusion: the nodal pattern of the hydrogen atom can be viewed as resulting from a double-slit interference along two principal ellipses. The interference determines the eigenenergies and the eigenstates. Even the notorious difficult-to-calculate van Vleck-Pauli-Morette (VVPM) determinant can be expressed in short closed form with the help of Lambert’s theorem and our result works even in higher dimensions. The analytic form of the action and the VVPM determinant becomes essential for our continuation of the classical action into the forbidden region, which corresponds to a tunneling process, see the last part of our paper.

Lambert is definitely a very fascinating person. Wouldn’t it be nice to discuss with him about philosophy, life, and science?